On this page, you will use recursion to draw the Lévy C-curve.
As in the snowflake algorithm, the base case for the Lévy C-curve is a single line segment:


At each next level, the algorithm draws two copies of the previous level, some percentage of the length of the previous level, and arranged in a right angle as shown below. (As before, the red shows a smaller version of the previous level.) You'll have to figure out how much smaller the size input should be in the recursive calls.
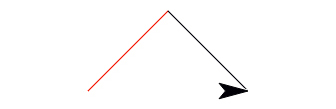

If the hypotenuse (the base case length) is size, what length must be given to the recursive call? Need another hint?
In the third level, the sprite again replaces each straight line with a pair of lines for a total of four smaller lines. Notice that the second and third lines form one long line. The red color here makes that visible. Your version should be all one color for now.


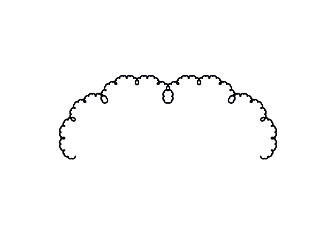
This simple algorithm builds up a complicated design at higher levels:
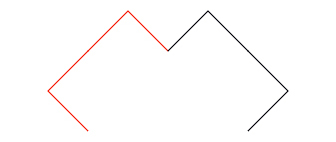

Look at the difference between the level 2 curve and the level 3 curve. Need another hint?
To make the level 3 curve, you must turn left (how much?), recursively draw a smaller level 2 curve (how much smaller?), turn again (which way? how much?), recursively draw another smaller level 2 curve, and then turn left.
What should your curve look like?
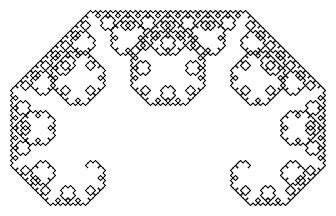
At level 12, the Levy C-curve shape will look like this: