7.1.3
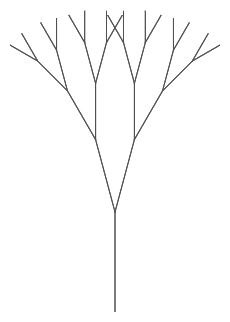
If this picture is drawn, what number must be in the
level input slot of the
tree procedure?
6
How many different sizes of line segment are in the picture?
1
How many different sizes of line segment are in the picture?
5
Nice! There are indeed five different levels present in the tree.
4
How many different sizes of line segment are in the picture?
7.1.3
What would happen if you changed the input size to be -100? (Don't use Snap!. The point is to think about it.)
The program will never stop running and a lot of different branches will be drawn.
The program will stop. Try running walking through the function step-by-step using the given inputs.
It will never stop running and only a single branch will be drawn.
The program will stop. Try running walking through the function step-by-step using the given inputs.
It will work just as if the size were positive 100.
Not quite. What happens when we plug in a negative value to the move block?
The image will be flipped upside down but will otherwise look the same.
Nice! Inputting negative values to the move block will make the sprite move backwards.
Nothing will be drawn.
Something will be drawn. Try running walking through the function step-by-step using the given inputs.
7.1.3
What would happen if you changed the input level to be -4? (Don't use Snap!. The point is to think about it.)
The program will never stop running, but it will draw a tree-looking tree with more and more smaller and smaller branches.
It's true that the program will never stop running. Try walking through the code step-by-step to see exactly what it draws.
It will never stop running, and the picture will be a leftward spiral with the sprite spinning around in midair.
Correct! The function will never hit the level = 1 case, and will only ever make the left-branch call to itself.
It will work just as if the level were positive 4.
Will the recursion ever reach level 1?
The image will be flipped upside down but will otherwise look the same.
Does the level input affect the move blocks?
Nothing will be drawn.
Something will be drawn.
7.1.4
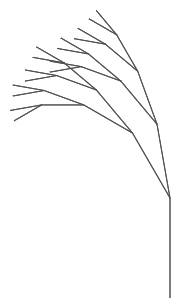
What was changed in the code?
The turn amount between branches
Correct!
The scaling factor (how much the length decreases each time)
Notice how the branches are now tilted differently from those in the original image.
Additional recursive calls to the function and additional turn blocks
There are still the same number of branches at each stage.
7.1.4
What was changed in the code?
The turn amount between branches
We did change angles here, but those are not the only changes we made. Where did those extra branches come from?
The scaling factor (how much the length decreases each time)
The branch lengths look pretty similar to the original.
Additional recursive calls to the function and additional turn blocks
Correct! There are now five recursive calls (branches).
7.1.4
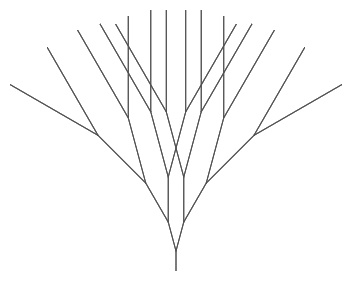
What was changed in the code?
The turn amount between branches
The angles look pretty similar to the original.
The scaling factor (how much the length decreases each time)
Right! At each stage, the branches are getting longer.
Additional recursive calls to the function and additional turn blocks
There are the same number of branches, and the angles haven't changed.
7.1.4
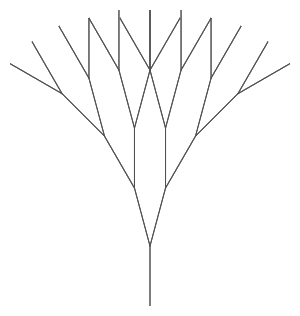
What was changed in the code?
The turn amount between branches
The angles look pretty similar to the original.
The scaling factor (how much the length decreases each time)
Right! At each stage, the branches are staying the same length, rather than shrinking.
Additional recursive calls to the function and additional turn blocks
There are the same number of branches, and the angles haven't changed.
7.1.4
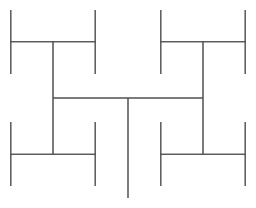
What was changed in the code?
The turn amount between branches
Correct! The turning angles are 90 degrees in this case.
The scaling factor (how much the length decreases each time)
It's a bit hard to tell, but the scale factor is the same as the original.
Additional recursive calls to the function and additional turn blocks
There are the same number of branches in this tree.