Unit 7 introduces recursion in the context of fractal graphics, i.e., pictures that include smaller versions of themselves. The canonical example is the fractal tree, in which each branch is a smaller sub-tree with branches of its own.Recursion is the use of a procedure within itself. The definition is simple, but learning to use recursion takes opportunity and practice; learning it well requires care in the order in which ideas are presented.
Unit 7 introduces recursion in the context of fractal graphics, i.e., pictures that include smaller versions of themselves. The canonical example is the fractal tree, in which each branch is a smaller sub-tree with branches of its own.
The work on trees walks students through steps that help them overcome the feeling that a recursive call is "cheating" because it uses a block that hasn't been fully written yet. To avoid this confusion, we start with a sequence of simpler (non-recursive) tree blocks, each of which calls the one before it (e.g., tree 2 calls tree 1; tree 3 calls tree 2; and so on.) A few students will want to jump immediately to the recursive version. Unless they are already quite comfortable with recursion from some other learning, it's worth going through this level-by-level once to feel the structure; starting on the next page they'll write recursive procedures directly.
The reason why we do not start with tail recursion, in which the sole recursive call comes at the tail end, like this
is that students often misunderstand the recursive call at the end to mean "go back to the beginning." This wrong mental model works for tail recursive blocks, but fails when students confront (or must design) a recursive call that can't be at the end of the definition. Embedded recursion, in which the recursive call isn't the last thing in the script, provides a more resilient introduction.
The repetition on page 1 of is deliberate: the tactile experience of building almost the same script repeatedly helps students notice its structure, and helps them see the virtue of combining them into a single script using recursion. Resist the temptation to teach them shortcuts, like duplicating scripts and adjusting them.)
Tree InputsTree Variations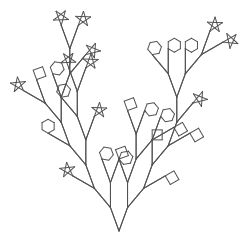
Vee project, which selects blocks to draw from a list of shape blocks that includes the vee block itself.Before starting the lab pages:This unit begins with a teacher demonstration because the collective gasp when the first complex picture appears is unforgettable. Vee is a great introduction to recursion because its use of randomness lets you ignore completely the annoying detail of base cases in recursive code. Students who've seen the demo, therefore, aren't ready to write their own recursive programs, but they're motivated to work through the first lab.
vee procedure does. Type the space key to show the block definition and discuss how the steps of the procedure generate the images that appear. Do not call students' attention to the fact that shapes is a list of blocks; if a student asks about it, just acknowledge that that's what it is.vee to the list of shapes?" Type the uparrow key to do this. You will likely hear answers such as "We'll sometimes get another v-shape on one of the ends."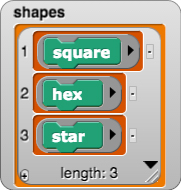
vee block called itself?" Don't worry about getting to a precise answer here; the idea is just to instill a sense of the power behind the simple process of calling a procedure from within itself.Note that the list of blocks in the corner of the stage (shown right) is something the students won't have seen before, but resist the temptation to talk about it. Students will come to understand it by themselves because they've seen lists before and they've seen blocks before.
tree 2 block definition together with an image of the result and ask students to describe the role of each block on the resulting drawing. Do the same for tree 3.tree?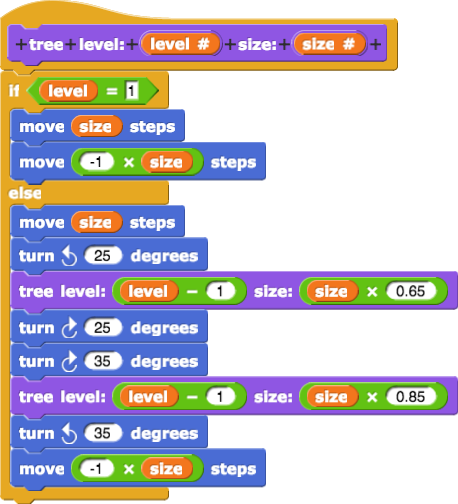
tree script and describing how recursion works in this script.tree are base cases.Tree Inputs.
Tree Variations.
These resources spend a lot of time with examples that could be done iteratively. They are provided as additional reading for teachers but not recommended for students.