Numbers and Computers

Consider cutting into two pages. --MF, 1/11/23
Next time around, we should add content to cover (maybe an extra page like 1.6.4, Emoji Deep Dive):

2-NI-05: Explain how physical and digital security measures protect electronic information. Information that is stored online is vulnerable to unwanted access. Examples of physical security measures to protect data include keeping passwords hidden, locking doors, making backup copies on external storage devices, and erasing a storage device before it is reused. Examples of digital security measures include secure router admin passwords, firewalls that limit access to private networks, and the use of a protocol such as HTTPS to ensure secure data transmission.

2-IC-23: Describe tradeoffs between allowing information to be public and keeping information private and secure. Sharing information online can help establish, maintain, and strengthen connections between people. For example, it allows artists and designers to display their talents and reach a broad audience. However, security attacks often start with personal information that is publicly available online. Social engineering is based on tricking people into revealing sensitive information and can be thwarted by being wary of attacks, such as phishing and spoofing.

--MF, 10/23/21
In this activity, you will learn how to use Snap! like a calculator and how computers store numbers.

Crunching Numbers

Snap! can do calculations just like a calculator. You can even nest operations inside each other, and they will behave just like when you use parentheses in a math expression.
() + () () - () () × () () / ()

  1. Open this Numbers Bits Electricity project, and save it to your account.
  2. Build and run each of the following expressions:
    1. 20 × 5
    2. (20 × 5) / 4
    3. 28 - ((20 × 5) / 4)

Notice that for the expression (20 × 5) / 4, the first input to the () / (4) block is the output of the 20 × 5 block (that is, 100), so this expression means (20 × 5) / 4.

Similarly for the expression 28 - ((20 × 5) / 4), the second input to the (28) - () block is the output of the (20 × 5) / 4 expression (that is, 25), so this expression means 28 - ((20 × 5) / 4). You can imagine the rounded corners of the blocks to be parentheses.

  1. Build Snap! expressions to calculate the following:
      55, 27
    1. 5 × (7 + 4)
    2. (11 – (48 / 6)) × 9
  1. Build Snap! expressions to calculate the following:
      239, 10
    1. (2 × (10^2)) + (3 × (10^1)) + (9 × (10^0))
    2. (1 × (2^3)) + (0 × (2^2)) + (1 × (2^1)) + (0 × (2^0))

Numbers Systems for Humans vs. Machines

CSP treatment of binary

The numbers you use in daily life are decimal numerals.

: Decimal Numerals

A decimal numeral is part of the base 10 system, the system we learn by counting on ten fingers.

In base 10, there are ten digits (0-9), and each place is worth ten times as much as the place to its right.

For example, consider the number 239...

2
3
9
100s place
10s place
1s place

The number 239 is equal to (2 × 100) + (3 × 10) + (9 × 1). You could write it in Snap! like this:
((2 × 100) + (3 × 10)) + (9 × 1) reporting 239
  1. Talk with Your Partner Describe each of the digits and their place values for the decimal numeral 2405.

Instead of counting on ten fingers, computers count with only two options: on and off. So, computers store numbers as binary numerals. All their calculations are in binary. They convert the decimal numerals we use to interact with computers into binary numerals before performing any calculations.

: Binary Numerals

A binary numeral is part of the base 2 system.

In base 2, there are two digits (0-1), and each place is worth twice times as much as the place to its right.

For example, consider the binary numeral 1010...

1
0
1
0
8s place
4s place
2s place
1s place

We can figure out the decimal equivalent by adding up all the places that have a one (that is, 8 + 2 = 10). You could write it in Snap! like this:
(((1 × 8) + (0 × 4)) + (1 × 2)) + (0 × 1) reporting 1010
  1. 39
    Talk with Your Partner Find the decimal representation for the binary numeral 100111.
    2. Need help reading binary?

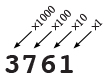    place values in decimal 3761: 3 1000's 7 100's 6 10's 1 1's In base 10 notation, each place value represents a power of ten: the units place (100 = 1), the tens place (101 = 10), the hundreds place (102 = 100), the thousands place (103 = 1000), etc. So, for example:

    3761   =   3 × 103  +  7 × 102  +  6 × 101  +  1 × 100

    place values in binary 10010: 1 16's 0 8's 0 4's 1 2's 0 1's Base 2 uses the same idea but with powers of two instead of powers of ten. Binary place values represent the units place (20 = 1), the twos place (21 = 2), the fours place (22 = 4), the eights place (23 = 8), the sixteens place (24 = 16), etc. So, for example:

    100102   =   1 × 24  +  0 × 23  +  0 × 22  +  1 × 21  +  0 × 20   =   16  +  2   =   1810

I think the above "reading" exercise should include a few more numbers and the below ITIT needs more support for writing in binary. --MF, 9/22/21
  1. Try writing a number in binary and see if a friend can convert back to your original number. If they have trouble, go through both calculations (yours and theirs) together. If they succeed in finding your original number, try a bigger number!
In this activity, you explored calculations in Snap! and learned to read numbers in binary representation.